Задачи на построение

Страница
1

Слайд 1

Задачи на построение

Геометрия 7 класс по Л.С. Атанасяну

Слайд 2

Слайд 3

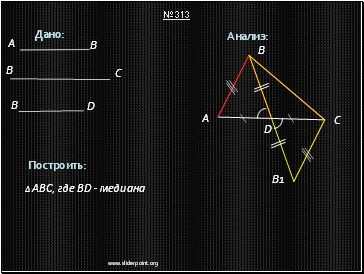
Описание построения

1. Строим ∆BCB1 по трём сторонам (BB1 = 2BD, CB1 = AB).

2. Строим точку D — середину BB1.

3.* На продолжении луча CD от точки D откладываем отрезок, равный CD (получили точку A).

4. Проводим сторону AB.

5. ∆ABC — искомый.

Задача имеет решение и при том только одно, если для отрезков AB, BC и 2BD выполняется неравенство треугольника.

Слайд 4

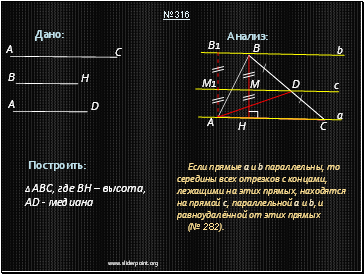
Если прямые a и b параллельны, то середины всех отрезков с концами, лежащими на этих прямых, находятся на прямой с, параллельной a и b, и равноудалённой от этих прямых

(№ 282).

Слайд 5

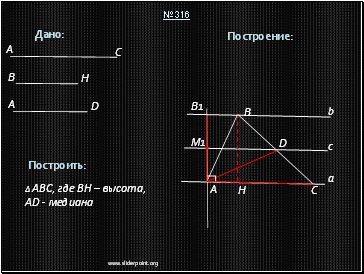
Описание построения:

1. Строим две перпендикулярные прямые (получили точку A).

• На одной из сторон прямого угла от точки A откладываем отрезок равный HB (получили точку B1).

3. От точки A на прямой a откладываем отрезок равный AC (получили точку C).

4. Строим точку M1 — середину отрезка AB1.

5. Через точку M1 проводим прямую c, параллельную прямой a.

6. Через точку B1 проводим прямую b, параллельную прямой a

7. Из точки A раствором циркуля равным AD проводим дугу до пересечения с прямой c (получили точку D).

8. Через точки C и D проводим прямую (получили точку B).

9. Проводим сторону AB.

10. ∆ABC — искомый.

Задача не всегда имеет решение. Если решение есть, то оно единственное.

Слайд 6

Слайд 7

Слайд 8

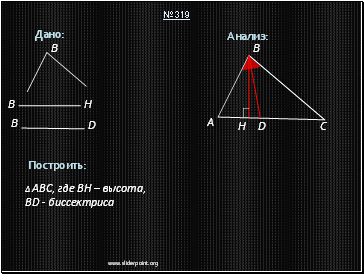
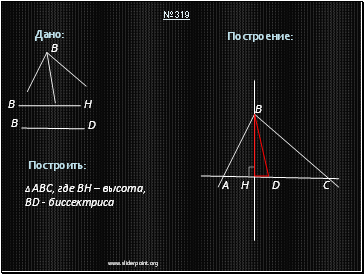
Описание построения:

1. Построим прямоугольный треугольник HBD по гипотенузе и катету.

• Проведём биссектрису данного угла B (получим угол ABD).

• Достроим угол DBH треугольника HBD до угла DBA, равного половине угла A (получим точку A).

4. Достроим угол ABD до угла ABC (получим точку C)

5. ∆ABC — искомый.

Задача всегда имеет решение и при том единственное.

Слайд 9