Решение задач на нахождение площади поверхности и объемов тел вращения

Страница
1

Слайд 1

Решение задач на нахождение площади поверхности и объемов тел вращения

Слайд 2

Найдите площадь поверхности (внешней и внутренней) шляпы, размеры которой (в см) указаны на рисунке.

Решение.

1) Если дно шляпы опустить на плоскость её полей, то получим круг радиуса

2) Площадь этого круга

3) Найдем площадь боковой поверхности цилиндрической части

4) Найдем площадь шляпы

Слайд 3

Задача 1.

Прямоугольный треугольник с гипотенузой

25 см и проведенной к ней высотой равной 12 см

вращается вокруг гипотенузы. Найдите площадь

поверхности тела, полученного при вращении.

Решение:

АВ=25 см, СН=12 см

Sтела=Sбок.кон(1) + Sбок.кон(2)

h2=ac*bc (высота в прямоугольном треугольнике)

CH2=AH*HB. Пусть AH=x, тогда НВ=25-x. x(25-x)=122; x2-25x+144=0; АН=16 см, НВ=9 см

Из ΔАНС по теореме Пифагора АС2=АН2+СН2;

АС=20см-(образующая 1) Sбок.кон(1)=πrl=π*12*20=240π (cм2);

Из ΔВНС СВ2=СН2+НВ2

CB=15 (см).- (образующая 2).

Sбок.кон(2)=π*12*15=180π (см2).

Sтела=240π+180π=420π (см2)

Ответ: 420π см2

Слайд 4

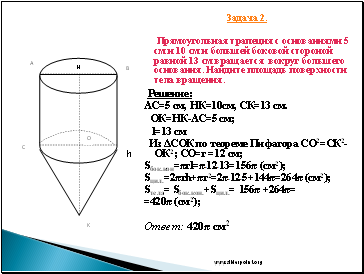
Задача 2.

Прямоугольная трапеция с основаниями 5 см и 10 см и большей боковой стороной равной 13 см вращается вокруг большего основания. Найдите площадь поверхности тела вращения.

Решение:

АС=5 см, НК=10см, СК=13 см.

ОК=НК-АС=5 см;

l=13 см

Из ΔСОК по теореме Пифагора СО2=СК2-ОК2; СО=r=12 см;

Sбок.кон=πrl=π*12*13=156π (см2);

Sцил.=2πrh+πr2=2π*12*5+144π=264π(см2);

Sтела= Sбок.кон.+Sцил.= 156π +264π=

=420π (см2);