Решение задач на нахождение площади поверхности и объемов тел вращения

Страница
2

Ответ: 420π см2

Слайд 5

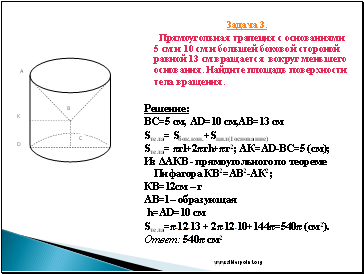
Задача 3.

Прямоугольная трапеция с основаниями 5 см и 10 см и большей боковой стороной равной 13 см вращается вокруг меньшего основания. Найдите площадь поверхности тела вращения.

Решение:

ВС=5 см, АD=10 см,АВ=13 см

Sтела= Sбок.кон.+Sцил(1основание)

Sтела= πrl+2πrh+πr2; АК=АD-ВС=5 (см);

Из ΔАКВ - прямоугольного по теореме Пифагора КВ2=АВ2-АК2;

КВ=12см — r

AB=l — образующая

h=AD=10 см

Sтела=π*12*13 + 2π*12*10+144π=540π (см2).

Ответ: 540π см2

Слайд 6

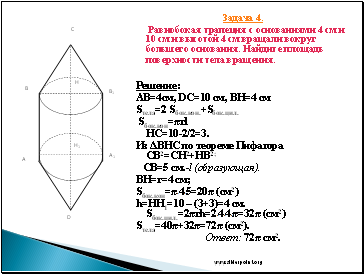
Задача 4.

Равнобокая трапеция с основаниями 4 см и 10 см и высотой 4 см вращали вокруг большего основания. Найдите площадь поверхности тела вращения.

Решение:

АВ=4см, DC=10 см, ВН=4 см

Sтела=2 Sбок.кон.+Sбок.цил.

Sбок.кон=πrl

HC=10-2/2=3.

Из ΔВНС по теореме Пифагора СВ2=СН2+НВ2;

CВ=5 см.-l (образующая).

BH=r=4 cм;

Sбок.кон=π*4*5=20π (см2)

h=HH1=10 — (3+3)=4 см. Sбок.цил.=2πrh=2*4*4*π=32π (см2)

Sтела=40π+32π=72π (см2).

Ответ: 72π см2.

Слайд 7

Слайд 8

Слайд 9

Слайд 10

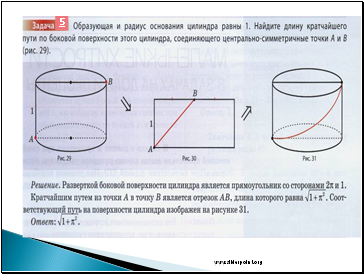
Дано два цилиндра. Объем первого равен 12 м3. Радиус

основания второго в два раза меньше, чем первого, а высота в три

раза больше. Требуется найти объем второго цилиндра.

Решение: Объем цилиндра вычисляется по формуле:V=hπr²

Отметим радиус основания первого цилиндра r а высоту h.

Тогда радиус основания второго цилиндра равен r/2, а